Steps in 31edo	Cents
1	38.71
2	77.42
3	116.13
4	154.84
5	193.55
6	232.26
7	270.97
8	309.68
9	348.39
10	387.1
11	425.81
12	464.52
13	503.23
14	541.94
15	580.65
16	619.35
17	658.06
18	696.77
19	735.48
20	774.19
21	812.9
22	851.61
23	890.32
24	929.03
25	967.74
26	1006.45
27	1045.16
28	1083.87
29	1122.58
30	1161.29
31	1200

Thirty One's a Crowd

You may have noticed that, when examining 12edo and related tunings, we stopped at primes 2, 3, and 5. While it's correct that this is enough to provide a vast amount of chord options, and we don't necessarily need more, adding in higher primes gives us access to significantly more color and vibrance in our music.

For example, pental major and minor thirds (based on 5), specifically 5/4 and 6/5, have a relaxed, warm quality to them, especially when tuned as accurately as they are in 31edo, with 5/4 being 386 cents, and 6/5 being 316 cents. Septimal thirds (based on 7) have a distinctly different quality to them, specifically the 7/6 minor third and 9/7 major third. These intervals are very unfamiliar, so they can sound dissonant to ears trained on 12edo, though because of the simple ratios, they sound consonant as they become familiar, so they're important options to have. The pure ratios are 267 and 435 cents respectively, with the minor having a more melancholy sadness to it, and the major with a dramatic "blaring" brightness.

The existence of two more types of thirds already provides opportunity for tons of unique chords, but 31edo rounds out this selection with a third right between the traditional major and minor, dubbed the neutral third. The standard JI ratio for the neutral third is 11/9, which 31edo nails within a cent. 11/9 is distinctly cold, much like many other simple 11-limit ratios, and makes for an unfamiliar, fairly dissonant type of triad. Melodically, it's very close to a type of "blue note" that musicians will bend to on some 12edo instruments, so having it as an actual note is useful.

JI Ratio	JI Cents	31edo Cents
3/2	701.96	696.77
5/4	386.31	387.1
7/4	968.83	967.74
9/8	203.91	193.55
11/8	551.32	541.94

Odd harmonics are the most important, as even ones are octave equivalent to a lower one, and 31edo represents the harmonics up to 11 quite accurately. 3/2 is slightly flat, though as seen before, a slightly flat fifth allows it to generate purer major thirds, and that's exactly what happens here. In fact, 31's fifth is just 0.2 cents off from the standard meantone fifth, allowing it to generate major thirds that are less than a single cent off, as opposed to 12edo's 14 cent difference.

The next lowest harmonic is the 7th, providing minor and major intervals with a unique character distinct from their 5-limit counterparts. And as it turns out, 7/4 is similarly tuned a single cent off, allowing these "subminor" and "supermajor" harmonies to sound equally pure. A key example is the harmonic seventh chord, represented as 1/1-5/4-3/2-7/4 or 4:5:6:7. It's a key part of many alternate tuning systems, and finds use in barbershop harmony as an alternative to the standard dominant seventh. Its simple ratios make it a premier resource in any 7-limit tuning landscape, so tuning it as accurately as 31edo does is important.

The 9th harmonic is tuned a bit flat due to the flatness of the meantone fifths stacking, though the 11th harmonic or 11/8 is tuned about equally flat, allowing ratios built from 3, 9, and 11 to be very precise, as seen with 11/9. This is important for playing many Arabic scales, which are often built primarily from these harmonics.

One way to characterize this inaccuracy in the 11-limit is the Quarter Comma System. The difference between the 5/4 and 81/64 thirds is the syntonic comma, or 81/80, so a quarter comma meantone fifth shaves a quarter of the syntonic comma off of each fifth. We can call the 31edo fifth, or 3rd harmonic, one quarter comma flat, the major third or 5th harmonic "pure", the 7th harmonic "pure", and the 9th and 11th harmonics two quarter commas flat. With this system, we see that every ratio between these harmonics is at most two quarter commas flat, with most being essentially pure or off by a quarter comma.

Notation

Alongside our five types of thirds comes five types of seconds, sixths, and sevenths, referred to as subminor, minor, neutral, major, and supermajor. In 12edo, you go from minor to major with a # or sharp sign, and major to minor with a b or flat sign, with x and bb for double sharps and double flats.

Because there's now a step between the two, we take a hint from some styles of Middle Eastern music and use half sharps and half flats. For example, in the key of A, the minor third is C and the major third is C#. So, the neutral third is Ct or C half-sharp. This extends to the subminor and supermajor, with Cd and C#t for C half flat and C supersharp/upsharp respectively. Conversely, Bdb would be B subflat or downflat.

In the key of G, a minor seventh chord includes the notes G Bb D F. Similarly, a subminor seventh chord includes the notes G Bdb D Fd, and a harmonic seventh chord includes G B D Fd.

To notate scale steps absent of a key, a common method is to preface a number with s for subminor, m for minor, n for neutral, M for major, S for supermajor, or P for perfect. For example, the major scale would be notated P1 M2 M3 P4 P5 M6 M7 P8.

The Diatonic Scale and Spiral of Fifths

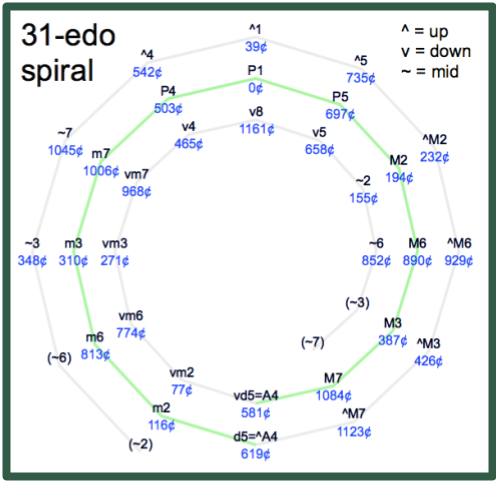
In 12edo, we can generate the diatonic major scale by taking any note and stacking five fifths above, and one fifth below. The same holds in 31edo, though the different size of the fifth makes the spacing different. The 12edo major scale has step sizes of 2212221, while in 31, it's 5535553, with whole tones at 5 steps out of 31, and diatonic semitones at 3 steps of 31, represented as 5\31 and 3\31 respectively.

Because the sizes of the whole tone and diatonic semitone are closer than in 12edo, the scale feels slightly smoother.

The increase in notes has another effect; the circle of fifths no longer is closed after 12 notes. The idea is still useful, however, so there are two options. We can use a 31 point circle, or use a spiral, with similar notes neighboring each other, as shown.